Сообщений в теме: 5823

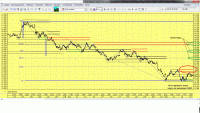
[sivka]

ТМВ щас на 140 и мы были на ней ровно вчера
но это на самом деле ни о чём ибо ТМВ движется вместе рынком - когда люди ребалансируются.
Конечно есть вероятность вернуться на 140, но не очень большая...
хотя раньше куккл любил закрывать ровно по страйку, вот и опытные люди о том же пишут
http://smart-lab.ru/blog/87191.php

СПСБ..

[sivka]

ТМВ щас на 140

А как же вот здесь??136 200?
о...не то посмотрела..Это цена последней сделки....

Сообщение отредактировал sivka: 13 ноября 2012 - 20:20

[Miklе]

ТМВ щас на 140 и мы были на ней ровно вчера
но это на самом деле ни о чём ибо ТМВ движется вместе рынком - когда люди ребалансируются.
Конечно есть вероятность вернуться на 140, но не очень большая...
хотя раньше куккл любил закрывать ровно по страйку, вот и опытные люди о том же пишут
http://smart-lab.ru/blog/87191.php

[sivka]

К счастью это не имеет никакого значения.

Э...к твоему может и не имеет..А другим хотелось бы знать.Предположительно.Ведь могут же супер-опционщики хоть что-то подсказать измельчавшим трейдерам..

Сообщение отредактировал sivka: 13 ноября 2012 - 19:16

[Француз]

арбитражёры...аууу..
Время Ч наступает..Где экспирироваться будем?

К счастью это не имеет никакого значения.

[sivka]

Опционщики-арбитражёры...аууу..
Время Ч наступает..Где экспирироваться будем?
Насколько я понимаю,у РИ ТМВ на 136 приблизительно..Так вроде пришли уже..

[Next]

Надеюсь,ты не купился..

не прошли же зону, так что держу шорт.

[sivka]

тормознули на нижней границе канала на днях

Ну это смотря по каким точкам строить..У меня выход на границу как раз на 134..И фиба там И нижняя граница расширяющейся формации наконец пробита..на объёме.Очень долго не могли пробить,ползли по ней,как улитка по склону..

Сообщение отредактировал sivka: 13 ноября 2012 - 16:26

[покупашка]

Кошку жалели и хвост рубили по частям..А потом увлеклись и хватили лишку..Как бы голову не отрубили сгоряча.. ..Вот случай,когда уровень смог задержать цену ненадолго..(ну всё же полчаса постояли)..Может потому,что внизу до 134...пустота..Где тормозить будем..???

тормознули на нижней границе канала на днях

[sivka]

покупать похоже надо.

Надеюсь,ты не купился..

[sivka]

Осталась зелёная..Эх..Отработать бы побыстрее..

Кошку жалели и хвост рубили по частям..А потом увлеклись и хватили лишку..Как бы голову не отрубили сгоряча.. ..Вот случай,когда уровень смог задержать цену ненадолго..(ну всё же полчаса постояли)..Может потому,что внизу до 134...пустота..Где тормозить будем..???

Сообщение отредактировал sivka: 13 ноября 2012 - 14:26

[amtop]

Нормально..с пятого раза загрузила..и в мелком размере.Больше сервер хостинга не берёт почему-то.А фиба-да...Внутридневной лой-на ней.Прошили её как на швейной машинке.А она удержала..Вопреки всем сомневающимся..

Размер нормальный..... и открывается быстрее существенно.... так даже лучче...

[sivka]

РИ.ЧАСЫ
137 860
137 800
137 400..
Целых три уровня почти сошлись..К тому же..нет ни перепроданности,ни дивергенции..Разворот не завершён..

Ну вот..
Осталась зелёная..Эх..Отработать бы побыстрее..

Сообщение отредактировал sivka: 13 ноября 2012 - 10:57

[sivka]

Нормально грузится.... А чего сказать хотела? Про фибу.. заколдаванную...?

Нормально..с пятого раза загрузила..и в мелком размере.Больше сервер хостинга не берёт почему-то.А фиба-да...Внутридневной лой-на ней.Прошили её как на швейной машинке.А она удержала..Вопреки всем сомневающимся..

[amtop]

ри.5М
Эх..не грузится с хостинга..почему-то..

Нормально грузится.... А чего сказать хотела? Про фибу.. заколдаванную...?

[Next]

покупать похоже надо. За весь контракт (месяц остался) ни одного существенного отскока. Фибу нарисовал на своем графике, выше должны быть от текущих.

Прикрепленные изображения

• 

Сообщение отредактировал Next: 12 ноября 2012 - 19:19

[sivka]

ри.5М
Эх..не грузится с хостинга..почему-то..

Сообщение отредактировал sivka: 12 ноября 2012 - 14:59

[Miklе]

Давай определимся..Это форум трейдеров...
.....
А не рассуждения о том ,как хорошо и удобно и выгодно сидеть в опционах.

Если это форум трейдеров, почему я не могу на нём популяризовывать опционы ?
в частности то как
хорошо и удобно и выгодно сидеть в опционах )

Сообщение отредактировал Miklе: 11 ноября 2012 - 15:11

[amtop]

Задачка на выходные.
Как изменится уровень воды в бассейне (повысится, понизится или останется неизменным) если из лодки, плавающей в нём, выбросить из неё в бассейн камень?
P.S. Эту задачу предложили трём великим физикам - Гаммову, Оппенгеймеру и Блоху.... все трое дали неправильный ответ.

Ребята! Правильный ответ такой: уровень воды в бассейне понизится.

В исходном состоянии уровень воды фиксируется, когда в лодке лежит камень. Плотность камня выше, чем плотность воды... Средняя плотность Земли примерно 5, 5 килограмма на кубический дециметр (на литр). Пусть для определённости (но без потери общности) наш камень весит 6 кг и объёмом 1 литр. Это значит, что для того, чтобы он плавал в лодке, лодка должна водоизмещать лишние 6 литров воды - столько, сколько весит камень. Плюс собственное водоизмещение без камня, разумеется.
Если взять и просто вынуть камень на берег, то осадка лодки уменьшится и... она всплывёт на эти 6 литров. В новом положении она будет вытеснять на 6 литров воды меньше. Соответственно этому на какую-то высоту уровень воды в бассейне понизится.
Если затем бросить этот камень в воду, он вытеснит только 1 литр воды... ровно свой объём. Больше он не может. Уровень воды при этом поднимется, но меньше, чем он перед этим опустился, когда камень вынимали из лодки на берег. Если стенки бассейна вертикальные, то в нашем примере - ровно в 6 раз.

2 Persey "....минус немного объёма погруженной в воду части лодки" - этот минус будет больше того плюса, который получается при бросании камня в воду... если стенки бассейна вертикальные, то ровно во столько раз, во сколько раз плотность камня больше плотности воды. Если стенки бассейна не вертикальные, то нужно вычислять с учётом изменяющейся по высоте площади бассейна ...но качественно ответ будет один - уровень воды понизится .
" ...и вытесняется объём воды= объёму камня" - да, правильно, но он будет меньше, чем тот объём, который вытеснялся лодкой, когда камень был в ней. В той же пропорции плотностей воды и камня.
"....не заданы параметры лодки- она может иметь массу меньше или значительно больше массы камня." Масса лодки нас не очень интересует, т.к. она остаётся неизменной. Сколько воды она вытесняла в начале задачи, столько и вытесняет в её конце - ровно столько, чтобы самой оставаться на плаву.... но с камнем (в нашем примере) - она вытесняет на 6 литров больше.... Начальные и конечные условия, относящиеся к самой лодке - одни и те же.... Рассмотри случай, когда сначала камень на берегу, а потом его либо бросают в воду, либо кладут в лодку.... Пожалуй, такое рассмотрение будет самым простым и красивым. Один из случаев как раз и будет соответствовать начальным условиям нашей задачи, а другой - конечным. Разницу сам сразу увидишь.

2 Urwald "Ответ однозначный уровень повысится, так как плотность камня больше плотности воды…"- это половина решения ... это и было бы правильным ответом, если бы изначально камень лежал на берегу.... Но у нас начальные условия иные - они очень хорошо описаны у тебя самого: "... а чтобы держать на плаву камень нужно больше вытесняемой воды" - Правильно - а эта вытесняемая вода (лодкой) в начале разве не поднимала уровень воды в бассейне на некоторую высоту? Ты всё правильно изложил до этого момента. И пример с водой абсолютно правильный. Если лодка плавает в бассейне, то для уровня воды в бассейне всё равно, куда её наливать - в лодку или в сам бассейн..... а когда она потонет - те более... задача не изменится...как говорят, она не будет иметь точки разрыва...скорость повышения уровня воды в бассейне не изменится...

2 Француз - ты уже и сам всё знаешь.... Только решение не очень красивое приведено... и оно не очень корректное. Я посмотрел его внимательно. Реrsey прав. Начиная со второй картинки - оно неверное. Посмотри сам: осадка (глубина погружения лодки) осталась неизменной - это правильно: лодке всё равно - нагружют ли её одним и тем же камнем сверху или тянут внизу, но там, на 2 и 3 рисунках, общая водоизмещённая (вытесненная) часть воды складывается из начальной водоизмещённой части лодки + объём камня… а уровень воды в бассейне показан неизменным. Это та ошибка, на которую обратил внимание Persey. Вторая и третья картинки должны были бы это отразить - уровень воды следовало бы показать слегка увеличившимся... Вся фишка в том, что здесь нужно учитывать два разнонаправленных процесса: один (бросание камня) повышает уровень воды в бассейне, а второй (вынимание камня из лодки) - его понижает. Один из них однозначно перевешивает. А на приведённых картинках вклад первого процесса (перенос камня в бассейн) никак не отражён. Хотя ответ формально правильный. По-сути, там неявно используется допущение, что якобы плотность камня много больше плотности воды.... и задача теряет свою изюминку. Вот если бы вместо камня был бы кусок льда - ответ не получился бы даже формально. Заведённый под лодку кусок льда выталкивал бы её вверх.....

Сообщение отредактировал amtop: 11 ноября 2012 - 17:37

[amtop]

Давай определимся..Это форум трейдеров .И пишем о трейдинге.Любого масштаба.Твои постоянные намёки,что все здесь занимаются ерундой и мелочами (я-в частности),а твои методы-супер и глобал..-это и есть распальцовка и дешёвые понты.
Я пишу о фибоуровнях и озвучиваю самые важные,на МОЙ взгляд.Ты задал вопрос.Я ответила.Удовлетворил он тебя или нет?И чем?Конструктивно..Без оценок моих действий.Свою ошибку признаю и сделки озвучивать больше не буду.

В свою очередь от тебя тоже хотелось бы получать полезную информацию.А не рассуждения о том ,как хорошо и удобно и выгодно сидеть в опционах.Просто ссылки на страницу биржи,куда ты имеешь обыкновение отправлять, не годятся..Важна трактовка.Можешь ли ты это сделать?Вопрос..
Я же не пишу-"Ребята,стройте фибы..Это так классно"..

Ты чего сердишься?.... Не сердись...
Никакой ошибки ты не делаешь, когда озвучиваешь позы или идеи.... мы ж для этого тут и собрались... разве нет? .... а возникла эта идея интуитивно или проявилась из графиков - не самое главное.... это ж только визуальный инструмент и попытка распознать знакомые образы в процессе их возникновения.... и чем раньше, тем ценнее....вот видим кусочек статуи, палец на ноге, допустим, и гадаем - что это будет: Венера Милосская или Баба с веслом.... доросла статуя до колена.... ну, думаешь - она... Венера.... чуть выше представишь - дух захватывает.... а тут тебе веслом по голове.... у нас ведь нет того уравнения, корни которого мы вычисляем..... А идея без позы - всё равно, что поза без идеи... но уже кое-что... или наоборот - видел чел идею... а позой не подкрепил... а почему?... что удержало?... понять это - это ж самое главное на будущее и есть.... .

Сообщение отредактировал amtop: 11 ноября 2012 - 11:45